The Conformational module consists of a series of algorithms
designed to study the conformational space of medium-sized organic
molecules.
Questions about Conformations
and Energy Profiles
How do I know I have the global minimum?
The only way to be sure you have the global minimum is to do
a systematic search with a very large/dense grid. For example,
increase the rotation count for sp3-sp3 carbon bond rotors from
the default of 3 to 10.
This is known to be very inefficient,
and chances are that if you have a non-trivial molecule you
may not have the patience required for this calculation to complete.
Our experience with medium (drug-size) organic molecules is that the
Monte-Carlo algorithm, in general, does a good job of finding
the global minimum.
See "How do I know my MC result is good?",
and "Is the global minimum the best minima?"
Is the systematic algorithm reproducible?
Yes, if you start from the same conformation.
In simple molecules the systematic algorithm is almost always inclusive
of all (important) minima. As molecules become more
complicated the default grid size, while likely correct
in finding all classes of minima, may skip some minima.
For example, the single "gauche plus-gauche minus" [-120,+120]
conformation of olefins might
bifurcate into multiple minima as steric bulk increases.
It is likely that one of the two new minima would be found
using the standard systematic approach. But 'which one' would
depend on the initial conformation.
Take for example this not-so-simple 1-dimensional rotation from
a real molecule which is nominally a 2-fold rotor
(with minima near 110, and 300).
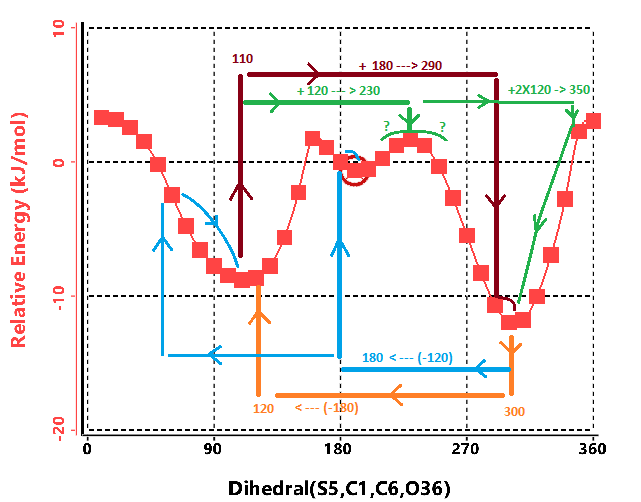
And recall that our algorithm is
- Start from the original structure
- rigidly move (or constrain in difficult cases) the relevant
dihedrals
- minimize to find "nearest" minima from this starting case
If we start from the
300-degree minima and assume a 2 fold rotation
our algorithm will take one 180 degree step to 120 and then minimize
to easily fine the minima at 110. Obviously missing the minima near 190.
Choosing a 3-fold rotor from
the same 300 degree starting point
we step to 180, very near the 190 minima, and to 60 which will the go
downhill to the 110 minima.
However, starting from the 110 degree minima is a different story.
The 2-fold rotor
will find only 1 other minima as expected.
Choosing the
120 degree steps of the 3-fold rotor
leads to a problem as the first step lands at a peak of 230 degrees.
And it seems like a 50/50 prospect of going to the 110 or 300 minima.
Thus making it likely that starting from this starting point would not
find the higher energy minima at 190.
Of course this story gets more complicated as the above energy
curve will change measurably for as other "nearby" dihedrals
change. (spinnage banging into other spinnage, or hydrogen bonding
stabilizing otherwise high energy conformerations etc.)
Thus my advice if you "want to find ALL minima" or
make the results "identical regardless of the starting point"
- You probably do not want to find ALL minima.
We believe our defaults find a reasonable sampling of
the low energy minima.
- Yet, if you really do want a fuller coverage of conformation
space you need to increase the fold count; ie for 3 fold
rotations use 4 or 5 knowing that this is overkill in many cases
and will greatly lengthen the job time.
Are Energy Profiles reproducible
Similar to the previous question; yes they are reproducible assuming
you start from the same conformation.
An example of the initial conformer affecting systematic
results can be found by inspecting an 8 member carbon chain:
"C1-C2-C3-C4-C5-C6-C7-C8". For illustrative purposes consider the
central "C4-C5" bond as we rotate it 360 degrees;
from -180 to
180 degrees. If one starts in the all "trans"
conformation, we find
that as we rotate the "C4-C5" bond the final conformation of
360 degrees is identical to the initial at 0 degrees. However,
if the initial conformation had a number of kinks in it, we
might discover that at the 120 degree mark, the C1 and C8
ran into each other. To relieve this steric problem the other
dihedral angles, will relax, likely changing by more than 100
degrees and falling into new energy wells. As we continue the coordinate
driving of the central C4-C5 angle to trans (180), we might find that
the final conformation is not the same as the initial conformation
because these other dihedrals have changed.
A contrived example of profile hysteresis
This kind of hysterisis is to be expected; the algorithm changes 1 degree
of freedom and then finds the "nearest" minimum with this constraint.
In complicated systems with multiple minima hysteresis like effects
can and do happen. A silly cartoon of how this can occur given an
ugly two dimensional energy map is shown below.
Going from one "blue minima" to the other is not reversible

The point of this graph on the left is that both the green path
and the yellow
path make some big jumps when the minima they are in is no longer
stable. If they were "quantum objects" they might tunnel through
that big red mountain separating them, or if they were
"good hikers" they might find the pass between the two red peaks.
(These paths paths are shown in the plot on the right.)
Is the global minimum the truth?
The global minimum is often the most interesting, and at the very
least, is often
representative of an equilibrium conformer found at room
temperature.
However, what conformation
is 'best' depends on what you are looking for. There are
often many other variables that conformational
analysis ignores, including the effect of solvent and the quality
of the energy reported at the given theory level.
How should I use QM methods with Conformation Analysis?
Because QM methods take more time than
molecular mechanics (by orders of magnitude), it is usually a mistake to try
conformational algorithms with QM methods. Typically, one
uses the MMFF mechanics force field to generate a list of low
energy conformers. This list is then resubmitted at the desired
QM level as either an "equilibrium geometry" or "single
point energy" calculation. The original MMFF conformers may
change geometry
slightly and their relative energies will likely differ.
For small systems (1 or 2 degrees of freedom) it is sometimes
possible to use conformational analysis to scan conformer space
with a QM method.
However, the time required, (as well as the possibility of bad
initial conformers with steric problems causing the breaking and
forming of bonds), require that users apply caution when
applying QM methods
to conformational analysis.
A further warning about "bad" initial conformers:
It is highly likely that in doing a full conformer search one may
start in an unfavorable position. For example, a gauche+/gauche+
conformer in propylene. At the beginning of the minimization two
hydrogens may be within 0.25 Angstroms of each other. With
molecular mechanics this "bad" starting position is
easily handled, but with
quantum chemical methods "chemistry" will occur;
resulting in the breaking and
reforming of bonds. You will likely not end up with the molecule
you
started with. Given that this is probably not what is intended,
and that it will
take a very long time to rearrange all atoms into a
"new" molecule, you will be lucky if the job runs out
of 'geometry
cycles' before taking up too much computer time. The
best approach is to "know"
that you are starting at a good conformer.
This is another reason why it is a good idea to start with MMFF
conformers.
This said, beginning in Spartan"18,
Wavefunction has introduced multi-step recipes taking advantage of the
strengths of both MM and QM models to provide accurate Boltzmann
distributions. Further, when utilized in conjunction with the
NMR Spectrum task, these also
provide a Boltzmann averaged NMR spectrum,. See the
Dealing With Conformationally Flexible Molecules
topic: Menu -> Activities -> Topics, from within Spartan.
How do I tell if the Monte Carlo results are correct?
The only way to know for sure is to compare results with a
complete, systematic calculation. (see How
do I know
I have the global minimum?.) You can build your confidence in
the Monte Carlo results by restarting the search from different initial
conformations.
If multiple starting points yield the same "global minimum" you should
have confidence that the algorithm is spanning the conformational space
fairly well.
What are the details of the algorithm?
- The conformation module has two modes:
Each of these algorithms consist of
moving or rotating one or more of the
molecule's bonds, followed
by a minimization. Each of these topics are
covered, in turn, followed by a short discussion of
how to customize the algorithm
and keywords:
-
SYSTEMATIC uses a systematic method to
explore the majority
of conformations of a molecule.
For acyclics, the algorithm rotates each bond by a specified angle (usually 120 degrees) and
searches for minima. This typically spans the conformational
space effectively
enough to find all conformations of small molecules. For cyclics, a
similar rotation (the Osawa rotation) is used to sequentially bend rings
within the molecule. However, the
conformations of rings are not necessarily well defined, and this may
not result in a complete search. For large molecules, this method
is time consuming, as the number of conformers searched
grows exponentially. For this reason, SYSTEMATIC
should only be used
for small, preferably acyclic, molecules.
-
MONTE CARLO uses a "simulated annealing" method to generate
conformations of a molecule. This procedure randomly rotates
bonds and bends rings until a preferential
(minimum energy) geometry is attained. Initially, the molecule is
considered to be a high-temperature system; this means that it
has significant energy and is flexible enough to move from a low
to high energy conformation. This is important because often
the global minimum may be very
different from the initial conformation. As more conformers
are explored, the temperature of the system decreases, making the
molecule less inclined to move out of low energy conformations,
thus looking "more closely" at other minima in the
nearby vicinity.
The algorithm is a standard simulated annealing algorithm with a
temperature ramp of
T = T(final) + K*(1-I/Imax)3
Some modifications have been made to avoid
dead-ends; if the system appears "stuck", the current conformer
will be replaced with a randomly picked (but previously
calculated) conformation. The new conformation is weighted via the
usual (normalized) Boltzmann criteria.
-
Moves:
The basic moves are the same for both Systematic and Monte Carlo
algorithms:
- Basic torsion rotation:
The basic move in conformational searching. This may have
undesired long range effects, such as greatly straining
(or breaking) rings. (this move is avoided in
rings.)
- Osawa wag:
2 correlated rotations that keep ring closure.
If 4 atoms (A,B,C,D) are connected in series, the atom C,
and everything connected to it is to rotated
around the B--D axis. (If required, rearrangement of large
flexible groups attached to atoms B and D will performed
internally.)
The 'Osawa wag' is the default move for atoms in a ring.
- 6-member flip:
For 6 member rings, if 2 (and only 2) opposite atoms are
selected they are flipped in pairs. This move switches
from one chair conformation to the other, making it
unlikely that one will find a twist-boat conformation
(typically much higher in energy).
If one wants to
catch the twist-boat conformations, select more (than the
default--2) atoms in
six member rings (and increase the WINDOW variable).
The FINDBOATS keyword does
this automatically by
choosing 3 of the 6 atoms to flip in a non-correlated way.
- Non-Planar flip:
Some (non-planar nitrogen) atoms with 3 bonds are also
"flipped". This can occur via a wag of one of the arms
(for non-cages) or an atom inversion. These moves are
indicated as an "Atom-Fold-Count" of 100. This
"Non-Planar flip" is sometimes combined with the Osawa wag
and is displayed as an Atom-Fold-Count of 103.
-
Minimization algorithm:
When using a molecular mechanics method a multi-step
minimization algorithm is used:
- A rigid rotation (or set of rotations) is applied the current
molecule. (see moves)
- A minimization is applied given the set torsion constraints.
- The constraints are relaxed.
- A second minimization is applied.
- The constraints are removed.
- A fast minimization is done to get a rough geometry.
- If the energy is too high or the geometry has diverged from
the goal geometry by more than 90 degrees the job is considered
to have failed.
- A final minimization is done to remove all residual forces on the
molecule.
If a semi-empirical or quantum mechanical conformation is requested,
steps 1 and 2 listed above are completed, followed by a minimization
at the requested quantum mechanics level.
How can I modify the algorithm?
Within the 'Set Torsions' mode, you can choose the bonds and ring
atoms
involved in the conformational search. This is done by
double-clicking on either the desired bond or atom. When a bond
or atom is selected for rotation, a type-in box will appear.
This box is used to enter the number of increments in the
rotation. For example, if the value of 3 is entered, rotations
of 0, 120
and 240 degrees will be applied. If you do not specify bonds
or ring atoms, Spartan will use heuristics to decide which elements are
relevant in
attaining new conformers. Unless you have some chemical insight
as to the
relevant rotatable members, Spartan's default selections will
typically provide good results. Additionally, several
keywords will modify calculation details.
What do the fold numbers mean in the Set-Torsions mode?
On bonds, the fold number is simply the number of gross
conformers. So for '3' there are assume 3 states, each
360/3=120 degrees apart. Thus each move is +- 120 degrees. A
fold number of 2 would mean two conformers, each +- 360/2=180 degrees.
On atoms the fold number contains more specific information.
An atom fold number of 3 means an
"Osawa wag" is preformed. (A 4 implies a
coupled Osawa wag in a cyclohexane like ring.)
In the case where the number contains 3 digits, the ones-digit
is either 3 or 0 for Osawa wag or no wag, respectively.
The hundred's digit, if present indicates that an inversion will
be tried.
This may occur on asymmetric, non-planar, trivalent
nitrogens.
Use the keyword PRINTLEV=2 when the job is run to see more
information on what precisely is being flipped and/or rotated.
Interpreting the output file:
Description of the columns:
Why does the output say it is
removing molecules from the list and how is it deciding
what to remove?
Any conformer that has an energy greater
than WINDOW
(10.0 kcal/mol) of the lowest energy conformer is thrown away. If there
are more than MAXCONFS (100)
conformers with acceptable
energies the program will discard conformers with
the goal of keeping as diverse a group as possible, while,
at the same time as
keeping the lowest energy conformers.
How many cycles will my molecule
take? or
Will my molecule use the Systematic or
Monte Carlo method?
The number of cycles a molecule will take depends on the
type and number of rotatable bonds. Each rotatable bond has a
fold number. (This fold number can be modified in the 'Set Torsions' mode.) For example sp3-sp3 bonds have a
default fold number of 3 because these bonds usually have 3
minima 120 degrees apart.
For systematic methods the number cycles is the product of all
the fold numbers.
For Monte Carlo methods the default
number of cycles is the square of
the sum of all folds. (This equation is a purely empirical
formula; experience has shown it to be adequate.) One can
limit this value to an upper limit using the
"Maximum Conformers Examined" field in the
setup panel, and increase the value above the default using the
McConfs= keyword.
The program will choose between the Systematic or Monte Carlo
method by choosing the one with the fewest default conformer
tries (unless the SEARCHMETHOD
keyword is used to override the default).
Support@wavefun.com


