These values are printed in the output. It should be noted that in the output two different equations are used to calculate polarizabilities. (E4 is the energy equations and 'dip' is the dipole equation--from the Kurtz paper.) The main difference between these methods is sensitivity to 'round off' error. The difference can be used as an estimate of the uncertainty in the final results. Note that the details are in the verbose output, so make sure to use the KEEPVERBOSE keyword or set the "Keep Verbose" option in the "Preferences Dialog".
These values are accessible from the spreadsheet with the
@PROP() possible options are:
electronegativity: -( E_HOMO + E_LUMO )/2
hardness : -( E_HOMO - E_LUMO )/2
polarizability : 0.08 * VdW_Volume
-13.0352*hardness + 0.979920*hardness^2
+41.3791
The final units are in
10-30 m3
Electron Densities, Spin Densities, Dipole Moments, Charges
and Electrostatic PotentialsTo get the more traditional units of coul2*m/N we divide by the permittivity of free space (and 4*π) and then scale to units appropriate for the atomic scale.
To convert from "au" (as calculated by the quantum calculations) to coul2m/N (or coul2m2/J) one must multiply by
1 a.u. = 16.4877x10-42 coul2*m/N
1 a.u. = 0.148185 A3
1 a.u. = 0.148185 m-30
1 a.u. = 0.373803244 cm3/mol
1 a.u. = (1/2.542) D (used in the numerical calculation)
For example an HF/6-31+G(2df) calculation of carbon monoxide gives
polarizability of "10" in the direction perpendicular to the
molecular axis, which is
1.65x10-40 coul2m/N, in fair agreement
with experiment (2+-0.5).
Where do the terms of the empirical polarizability formula come from?
Though these
coefficients may appear arbitrary, the first term
is derived from an estimation that assumes all atoms have the
polarizability of hydrogen,
with a correction applied from the energy gap of the highest occupied &
lowest unoccupied molecular orbitals. This equation is only used in the
semi-empirical methods--and it turns out that this is a fairly good
first guess. From a freshman physics textbook, the answer should
be (for atomic groups):
H 0.66
He 0.21
Li 12
Be 9.3
C 1.5
Ne 0.4
Na 27
Ar 1.6
K 34
Q-plus & Q-minus are known as the 'TLSER' parameters.
Back to Top
O = A/(4*pi*((3*V)/4*pi)^(2/3))
where
A : Area
V : Volume
O : Ovality
Thus the He atom is 1.0 and HC24H (12 triple
bonds) is ~1.7.
| electronegativity | = -(HOMO + LUMO)/2 |
| hardness | = -(HOMO - LUMO)/2 |
In the QSAR panel of the "Molecule Properties" dialog we show a few volume/area related properties, and these fall into two categories: "From CPK Model" and "From Electron Density".
"logP" methods can be selected with the LOGP= keyword;
LOGP=VILLAR and LOGP=GHOSE
respectively.
An example Spartan file shows some of these logP examples on a broad range of simple molecules. While one can argue over which of these calculations is most precise or efficient, the noise in all these methods is typically smaller than the uncertainty in using LogP to predict common properties like blood/brain barriers.
Spartan includes a number of ways to examine solvation.
The default solvation model which we advise for geometry and frequency calculations is the C-PCM model (Conductor like Polarizable continuum model). This depends on the shape and charge distribution of the molecule (solute) and the dielectric of the solvent.
Continuum models such as C-PCM do not account for explicit solvent-solute interactions such as hydrogen bonding or 'explicit hydrophobic'. For this reason we do not report an "energy of solvation".
Spartan gives easy access to three different dielectrics: "NonPolar" (7.43 same as THF), "Polar" (37.22, same as dimethylformamide), and "Water" (78.3). From the pull-down menu in the Calculations dialog. You can add a different solvent by appending a dielectric constant or a solvent name, i.e.:
Some references for C-PCM models are:
There is a large and diverse literature on C-PCM methods. Spartan's defaults are recommended as these have been tested and are reasonable for organic systems. However for those familiar with the C-PCM literature we allow some access to the variations. There are 3 main "methods" to treat the polarizable continuum. One can replace the CPCM in the SOLVENT= keyword above with
SSVPE has been argued to be the best method for solvated excited states. an example of using SSVPE that might be appropriate for excited states is
There are a number of other parameters that can be changed in C-PCM models and can be added as comma separated options appended to the keyword after the dielectric. These are:
We currently implement the Cramer-Truhlar SM5.4P and SM5.4A solvation methods for water, and these are available for any molecule with SM5 parameterized atoms.
This is a very fast method and is appropriate to get quick "energy of solvation" energies at a given geometry. To use this model, for "solvation energy" calculations use the SM54 keyword in the option line.
The energy of solvation predicted by this model can be
found in the output text. You can print this in the
spreadsheet with the equation
In Spartan "10 and Spartan "14 this calculation was done by default for all HF and DFT jobs.
Literature on these methods is extensive,
some important articles are:
SM5.0R is a solvation method derived from the semi-empirical SM54 approach described above. It is independent of the wave function and depends only on the geometry of the molecule. As such, it is very fast and is applicable to large systems and molecular mechanics calculations. This method can be accessed by using the POSTSOLVENT=SM50R keyword.
MMFFaq is an extension to the MMFF94 forcefield, in which the SM50R energy term is added to the molecular mechanics energy. In Spartan, the MMFFaq force field is implemented such that the solvation energy is only added AFTER the geometry has been optimized. Thus the structures of molecules from MMFF94 and MMFFaq calculations will be the same, but their energies will be different. The MMFFaq method is most useful in the context of conformational searching or in an energy profile as the energy ordering of any conformers will likely be different in water (MMFFaq) than in vacuum (MMFF94).
The reference for SM5.0R is
The SM8 model allow both water and a number of organic solvents and treat both neutral and charged solutes. This method is notable for the large suite of experimental data used to parameterize the model and can be used with both HF or DFT wave-functions. To run SM8 as a property calculation (to calculate the energy of solvation) use the keyword POSTSOLVENT=SM8:WATER where water can be replaced with many different organic solvents. These methods are dependent on the basis set, and are parameterized for the 6-31G* sets. (While the method will function for other variants in the 6-31G series, experience has shown that using larger basis sets worsens the results.)
Technically, it is possible to do geometry optimizations with these models, but because of the discontinuous nature of the derivatives (due to the SCF like nature of solvated charge calculation) optimizations and frequency are problematic except for the simplest of molecules. Use the SOLVENT=SM12:WATER keyword for optimizations. (When you type in this keyword and hit 'enter'; the keyword will replace the "in Gas" pull-down menu in the upper right of the Calculations dialog.)
For SM8, SM12 and SMD you can use a number of different solvents
in place of water. The list of supported solvents follows:
WATER,
111TRICHLOROETHANE,
112TRICHLOROETHANE,
11DICHLOROETHANE,
124TRIMETHYLBENZENE,
14DIOXANE,
1BROMO2METHYLPROPANE,
1BROMOPENTANE,
1BROMOPROPANE,
1BUTANOL,
1CHLOROPENTANE,
1CHLOROPROPANE,
1DECANOL,
1FLUOROOCTANE,
1HEPTANOL,
1HEXANOL,
1HEXENE,
1HEXYNE,
1IODOBUTANE,
1IODOPENTENE,
1IODOPROPANE,
1NITROPROPANE,
1NONANOL,
1OCTANOL,
1PENTANOL,
1PENTENE,
1PENTYNE,
1PROPANOL,
222TRIFLUOROETHANOL,
224TRIMETHYLPENTANE,
24DIMETHYLPENTANE,
24DIMETHYLPYRIDINE,
26DIMETHYLPYRIDINE,
2BROMOPROPANE,
2CHLOROBUTANE,
2HEPTANONE,
2HEXANONE,
2METHYLPENTANE,
2METHYLPYRIDINE,
2NITROPROPANE,
2OCTANONE,
2PENTANONE,
2PROPANOL,
2PROPEN1OL,
3METHYLPYRIDINE,
3PENTANONE,
4HEPTANONE,
4METHYL2PENTANONE,
4METHYLPYRIDINE,
5NONANONE,
ACETICACID,
ACETONE,
ACETONITRILE,
ANILINE,
ANISOLE,
BENZALDEHYDE,
BENZENE,
BENZONITRILE,
BENZYLALCOHOL,
BROMOBENZENE,
BROMOETHANE,
BROMOOCTANE,
BUTANAL,
BUTANOICACID,
BUTANONE,
BUTANONITRILE,
BUTYLETHANOATE,
BUTYLAMINE,
BUTYLBENZENE,
CARBONDISULFIDE,
CARBONTET,
CARBONTETRACHLORIDE,
CCL4,
CHLOROBENZENE,
CHLOROTOLUENE,
CIS12DIMETHYLCYCLOHEXANE,
DECALIN
CYCLOHEXANE,
CYCLOHEXANONE,
CYCLOPENTANE,
CYCLOPENTANOL,
CYCLOPENTANONE,
DECANE,
DIBROMOMETHANE,
DIBUTYLETHER,
DICHLOROMETHANE,
DIETHYLETHER,
DIETHYLSULFIDE,
DIETHYLAMINE,
DIIODOMETHANE,
DIMETHYLDISULFIDE,
DIMETHYLACETAMIDE,
DIMETHYLFORMAMIDE,
DMF,
DIMETHYLPYRIDINE,
DMSO,
DIMETHYLSULFOXIDE,
DIPROPYLAMINE,
DODECANE,
E12DICHLOROETHENE,
TRANS12DICHLOROETHENE,
E2PENTENE,
ETHANETHIOL,
ETHANOL
ETHYLETHANOATE,
ETHYLMETHANOATE,
ETHYLPHENYLETHER,
ETHYLBENZENE,
ETHYLENEGLYCOL,
FLUOROBENZENE,
FORMAMIDE,
FORMICACID,
HEXADECYLIODIDE,
HEXANOIC,
IODOBENZENE,
IODOETHANE,
IODOMETHANE,
ISOBUTANOL,
ISOPROPYLETHER,
ISOPROPYLBENZENE,
ISOPROPYLTOLUENE,
MCRESOL,
MESITYLENE,
METHANOL,
METHYLBENZOATE,
METHYLETHANOATE,
METHYLMETHANOATE,
METHYLPHENYLKETONE,
METHYLPROPANOATE,
METHYLBUTANOATE,
METHYLCYCLOHEXANE,
METHYLFORMAMIDE,
MXYLENE,
HEPTANE,
HEXADECANE,
HEXANE,
NITROBENZENE,
NITROETHANE,
NITROMETHANE,
METHYLANILINE,
NONANE,
OCTANE,
PENTANE,
OCHLOROTOLUENE,
OCRESOL,
ODICHLOROBENZENE,
ONITROTOLUENE,
OXYLENE,
PENTADECANE,
PENTANAL,
PENTANOICACID,
PENTYLETHANOATE,
PENTYLAMINE,
PERFLUOROBENZENE,
PHENYLETHER,
PROPANAL,
PROPANOICACID,
PROPANONITRILE,
PROPYLETHANOATE,
PROPYLAMINE,
PXYLENE,
PYRIDINE,
PYRROLIDINE,
SECBUTANOL,
TBUTANOL,
TBUTYLBENZENE,
TETRACHLOROETHENE,
THF,
TETRAHYDROFURAN,
TETRAHYROTHIOPHENEDIOXIDE,
TETRALIN,
THIOPHENE,
THIOPHENOL,
TOLUENE
TRANSDECALIN,
TRIBROMOMETHANE,
TRIBUTYLPHOSPHATE,
TRICHLOROETHENE,
TRICHLOROMETHANE,
TRIETHYLAMINE,
UNDECANE,
Z12DICHLOROETHENE
It is important to note that no spaces are allowed in the name, thus "acetic acid" is spelled "ACETICACID".
SM12 has been defined for multiple charge models. The default uses Charge Model 5 (CM5) but Merz-Singh-Kollman (MK) and ChElpG (CHELPG) charges are also available. You can access these by adding to the end of the POSTSOLVENT= keyword. For example:
Some useful reference are
(In Spartan'14 this was called SS(V)PE but has been renamed to distinguish it from the SS(V)PE variants of C-PCM model
The Surface and Simulations of Volume Polarization for Electrostatics (SS(V)PE) method treats the solvent as a continuum dielectric, solving Poisson's equation on the boundary. A dielectric constant is needed for the calculation. For example, POSTSOLVENT=ISOSVP,78.39 would be used for water. References for this method can be found in
It should be noted that analytical gradients are not available, so transition state optimizations with this solvent model should only be applied to small molecules. Another important constraint of our implementation is that only molecules with 'star-like' volumes are allowed. Any ray emanating out from the center can only pass through the surface once.
Our implementation has been designed for small molecules. So for larger molecules one may have to modify internal parameters to get good results. Specifically NPTLEB=, which controls the number of Lebedev points set to 1202. This has been shown to be precise enough for .1 kcal/mol on solutes the size of monosubstituted benzenes. Possible values are: (974,1202,1454,1730,2030,2354,2702,3074,3470,3890,4334,4801,5294).
We use the POSTSOLVENT keyword to do an energy of solvation calculation. This calculation is useful to determine the energy differences among different conformers of the same molecule as the bond lengths and angles do not change significantly when solvent is added.
If one wants to see the effect of solvation on the geometry, (for example for a transition state structure) the ADDSOLVENT= or SOLVENT= should be used. SOLVENT= is a synonym for ADDSOLVENT=. When typed in, it will be erased (following pressing the Enter/Return key) from the Options line and the "in-solvent" pull down menu will be updated to reflect the specified solvent.
A longer discussion of how the solvation energy is calculated can be found under solvation methods in the "Quantum Mechanics Energy FAQs".
The Cramer-Truhlar methods (SM8, SM54, SM50R, SM3) work only with common organic atoms: H, C, N, O, F, S, Cl, Br, and I. (SM8 adds Si and P if bonded to oxygen.) SM12 covers the entire periodic table. The calculation may proceed with other elements, but important terms of the approximation will be set to zero. If the atoms "aren't very important" relative solvation energies of conformers might be useful, but absolute values will be poor.
In principle the C-PCM and SS(V)PE methods are not parameterized and are available for any atom of the underlying basis-set, however they do require atomic radii to generate the cavity. The atoms H-Ti, Cu-Sr, Ag, In-Ba, Pt, Au, Tl-Ra. have pre-defined values. By default we use the "Bondi Radii" increased by 20% to construct the cavity in the PCM solvation calculation. These are vdW radii originally proposed by Bondi, verified by Rowland and Taylor and extended by Cramer and Truhlar:
If alternate atoms are required you can use the PCMRAD= keyword. For example to use a Radii for Iron of 2.2 angstroms one would use PCMRAD=FE~2.2 If there are multiple atoms you can comma separate them. ( i.e.: PCMRAD=FE~2.2,NI~2.2 ) These "user radii" are the radii before being scaled by 20%. The 1.2 scale factor can be overriden with the PCM_VDW_SCALE keyword. The default value for this keyword is PCM_VDW_SCALE=1200000 (multiplied by 10-6 to become the actual value used.)
In more recent versions of Spartan, the output includes two sets of electrostatic charges. The traditional method calculates a charge for each atom. The newer method places a charge, a dipole, a quadrapole and an octopole on each heavy atom. (We are using these values in internal projects.) The use of atomic dipoles does a better job of modeling the electrostatic potential.
Spartan's ESP charge calculation is based on the 'CHELP'
algorithm.
In this algorithm the charges at the atom-centers are chosen
to best describe the external field surrounding the molecule.
Ideally this area should include everything outside of the van der
Waals radii. Of course this would be time consuming and may
work too hard to get very exact long-range dipole terms at the
cost of inaccuracies in the field near the atom. As a compromise,
a shell surrounding the atoms is used. The thickness of this shell
is 5.5 au. This default value can be modified using the
SHELL=
keyword in the Options field of the Calculations dialogue.
You may also change the inner value of this shell from the VDW
to (VDW + WITHIN) with the keyword
WITHIN=.
Relevant references:
More information from NBO calculations can be printed with the keyword PROPPRINTLEV=2. This keyword may be useful if you are interested in atomic hybridization of each atom or problems are detected with the NBO calculation.
Spartan's version of natural bond order attempts to find the "natural" Kekule bonding of each molecule. As such it has issues with delocalized systems. When strong delocalization is detected the calculation will not complete, but one can force the calculation to complete by adding the PROP:IGNORE_WARN keyword (and the PROPRERUN keyword to force the properties module to rerun). In this case the atomic polarization will likely be useful, but the total natural bond order is not to be trusted.
The overlap matrix is the overlap of different atomic orbitals. It can be printed with the PRINTOVERLAP keyword. The ordering of the coefficients is the same as that displayed for the molecular orbitals when the PRINTMO keyword is used.
<S2> is the spin operator, and it is relevant in UHF calculations. While UHF (or ROHF) is required for open shell systems and to get certain bond separation energies correctly, it suffers from the disadvantage that its wave functions are not (exact) eigen-functions of the total spin operator. This is because the UHF ground state can be contaminated with functions corresponding to states of higher spin multiplicity.
<S2> is a measure of spin contamination and is often used as a test of how good the UHF wave function is. Singlet states should have a value of 0.0, doublets 0.75, and triplets 2.0. If <S2> is within +- .02 of these values the wave function is usually considered acceptable.
The <S2> is printed out when the PROPPRINTLEV=1 keyword is used, and is represented in the output file as <S**2>
The default masses are found in the "MASS.spp" parameter file. ("params.MASS" on Linux machines.) The default value is the mass of the most common isotope. This can be overridden with the ISOTOPEMASS=AVERAGE keyword, or by changing the isotope of a specific atom in the Atom Properties dialogue.
To recalculate the "mass weighted hessian" with different masses the job must be re-submitted. Add the keyword PROPRERUN to force the property module to rerun without recalculating the energy
The strength of RAMAN frequencies are calculated from the change in polarization of the molecule with respect the vibrational mode. As such, this can be much slower than just calculating standard IR intensities (dependent on the change in the dipole). It should be noted that the Intensities shown in the "Output Summary" and plotted in the RAMAN graphs are scaled by the laser frequency [vo] (which can be changed in the Options menu -> Preferences -> Settings dialogue), plotted logarithmically and broadened with a Lorentzian.
The units of absorbance is kilometers per mol, km/mol. The justification for this unit can be surprising, so we derive this unit here. The molar absorption coefficient e
where C is the concentration, (mol/L), d is the path length (cm), Io/I is the intensity ratio (unitless, incident over transmitted) and 'v' is the wavenumber (1/cm). Thus the unit is
However, what is measured is the integrated absorption A
Spartan can generate a reaction path using three approaches. The simplest is via the 'Energy Profile' calculation, which changes specific coordinates. (See the discussion of energy profile.) This works well for simple systems when the reaction coordinate can be well represented as internal coordinates (such as bond distance).
A reaction path can also be generated by the calculation of the Transition State Geometry along with a frequency calculation. A list file can be generated for the single imaginary frequency corresponding to the reaction coordinate.
Spartan has also implemented a reaction coordinate algorithm to generate a reaction path given a transition state using the algorithm by Schmidt. (M.W. Schmidt, M.S. Gordon, M. Dupuis, J. Am. Chem. Soc. (1985), 107, 2585) This can be specified by selecting the IRC checkbox when performing a transition state geometry calculation. When selected, a new file will be generated that contains the reaction path. The IR check box should also be selected. If you know you have a good transition point and a good Hessian the IRC can be run as a single point "Energy" calculation with the BE:IRC keyword.
The IRC calculations are time consuming. It is suggested that users confirm that a 'good transition state' has been found before resubmitting the with the IRC algorithm enabled. Confirm both, that the gradient is small and that there is only 1 negative eigenvalue.
Keywords related specifically to IRC calculation can be found in the keyword section.
Spartan offers a number of ways to work with excited states, of varying complexity and cost. However, since nearly all ground states are singlets, and the first excited state is almost always the lowest triplet the easiest thing to do is look at the "Ground State" with two unpaired electrons. This is almost always "accurate enough" and much faster than any of the more advanced methods.
As an example consider benzene. The ground state was optimized. The HOMO-LUMO gap of 6.6 eV for this singlet would be a first approximation of the excited state energy. This molecule is copied+pasted in the spreadsheet and is submitted as a triplet. This is done twice, once with a triplet optimization, once at the same singlet geometry. The energy gain going from singlet to triplet is shown in the “Rel. E(eV)” column (notice highlighted equation). The single point energy would be the appropriate number for fluorescence (vertical excitation), and the triplet optimization would be for phosphorescence.
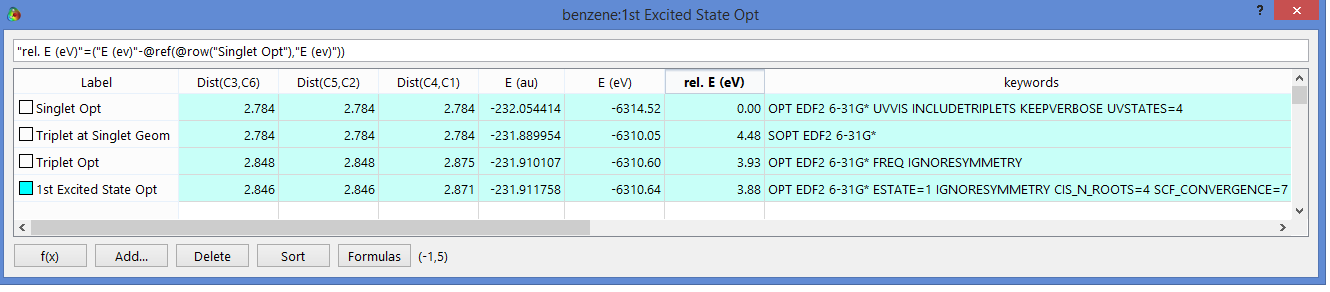Notice for the triple opt., symmetry is turned off with the
IGNORESYMMETRY keyword and the IR box is checked
(which becomes the FREQ keyword) to ensure one finds the
real triplet minimum.
Any negative frequencies would indicate that symmetry was not
sufficiently broken.
As an example of a different approach/theory, a UV/Vis calculation was run on the ground-state singlet (the UVVIS keyword). Also added were KEEPVERBOSE and INCLUDETRIPLETS, as mentioned in our help content. Additionally added was UVSTATES=4 because benzene is a difficult case, meaning poor convergence. If one examines the verbose output it is shown that using full TDDFT theory, the excited state energy (vertical excitation) is 3.88 eV (the TDA approximation gives 4.24 eV).
...TDDFT is probably better ..... needed for other excited states or singlet->singlet transitions.
We can do optimizations at the TDDFT level, as shown in the final row. These can be very slow (prohibitively slow for DFT functionals where analytical gradients are not available, as is the case for EDF2).
The UV/Vis spectra is calculated by running a single point CIS calculation (or TD-DFT calculation for DFT methods) after the main wave function has been calculated. In CIS theory, the absorption energies are the difference between the HF ground state and CIS excited state energies. A reference for Spartan's CIS implementation:
J.B. Foresman, M. Head-Gordon, J.A. Pople, M.J. Frisch, J. Phys. Chem. (1992), 96, 135.
For DFT calculations, excited states are obtained using the time-dependent density functional theory (TD-DFT) approach to generate excited states from excitations of the ground state molecular orbitals. The Tamm-Dancoff approximation (TDA) is also available to speed up the calculations:
E. Runge, U. Gross, Phys. Rev. Lett. (1984) 961533] A CIS-like Tamm-Dancoff approximation [S. Hirata, M. Head-Gordon, Chem. Phys. Lett. (1999) 302 375S.
Hirata, M. Head-Gordon, Chem. Phys. Lett. (1999) 314 291
This calculation is similar to the CIS calculation, and most keywords controlling the excited state CIS calculation are used in the TDDFT calculation.
A UV/Vis calculation is done, by default, whenever a single-point excited state calculation is specified. If one needs to modify the UV/Vis calculation, (other than with the UVSTATES keyword) a single point excited state calculation must be performed, using the keywords described below.
See the keyword section on CIS/TDDFT for relevant keywords. If you want a geometry optimization for something other than the first excited state, use the ESTATE=n keyword to choose a different excited state. (Note that when you hit the "Enter" key the ESTATE keyword disappears and the n appears where the "First Excited" in the first line of the calculations dialogue.
Often you may want the first excited singlet state, which may or may not be the actual first excited state. To limit the search of possible excited states to singlets you can type in the keyword CIS_TRIPLETS=FALSE.
Assuming that the real ground state is a singlet, and the first excited state is not a triplet, these both refer to the same electronic state. A difference exists in how Spartan calculates these; excited state calculations use either CIS or TDFT methods while ground state calculations use HF or DFT methods. The later may not be as accurate, but are much faster, especially in the context of geometry optimizations.
It is also possible that the first excited state is another singlet, and not a triplet. If in doubt you can do an energy calculations with the "UV/Vis Spectrum" and the INCLUDETRIPLETS keyword to examine all the excited states. Note that the description of singlet/triplet is found in the verbose output so you will need to add the KEEPVBOSE keyword. Graphically, the intensity of the singlet to triplet will be very small.
It should be noted that information on each excitation can be found in the verbose output. The notation:
The Transition dipole moment and oscillator strength are also printed. The oscillator strengths are used by Spartan to graphically display the UV/Vis spectrum. To convert the oscillator strength to absorbance, we divide by 4.319x10-7. Usually the log (base 10) of the absorbance is used to display the spectrum.
By default only pairs of filled/unfilled orbitals which have amplitudes larger than 0.15. To see more components you can use the CIS_AMPL_PRINT=1 keyword to see (nearly) all of the components. The sum of the square of all components will sum to 1.0.
Spartan supports calculation of chemical shifts for closed shell (systems with zero unpaired electrons), based on the Kussmann Ochsenfeld linear scaling algorithm using "gauge-including atomic orbitals" (GIAOs):
Chemical shifts are given in parts-per-million (ppm) relative to the appropriate standard (nitromethane for nitrogen, fluorotrichloromethane for fluorine, and TMS for hydrogen, carbon and silicon). These relative shifts are available for most common DFT functionals and basis sets. One can edit the "NMR_References.spp" file found in the Spartan shipping directory to add new standards.
Spartan can also apply systematic corrections to the Carbon NMR depending on the nearby chemical environment. These are referred to as "corrected shifts" in Spartan.
By default we use modified Karplus equations to predict hydrogen coupling constants:
Recently we have also added a feature to calculate scalar coupling constants (J-coupling) from first principles. For "non range-seperated" DFT functionals (i.e. B3LYP works, wB97X-D doesn't) we can calculate coupling constants (J) by directly calculating the indirect coupling tensor. This can be done from the Calculations dialogue, if one specifies Coupling Contacts as Calculated (Fermi Contact). This will utilize the PCJ-0 basis set. This is usually great for 3+ bond coupling, and "good enough" for 2 bond coupling. Larger basis sets (PCJ-1 or PCJ-2) are available, but take significantly longer (and may have difficulty converging for large systems) and are typically not worth it for 2 and 3 bond coupling. To run the "Full" ISSC calculation using the FC, SD, PSO and DSO contributions you can specify this via the keywords: JISSC=FULL,PCJ-1 or JISSC=FULL,PCJ-2.
The NMR calculation has its own set of SCF convergence issues. Usually the default parameters are good enough to get reasonable answers, but at times you may need to change these to get difficult systems to converge. The first thing to do is to make sure the integrals are more accurate than usual by typing the CONVERGE keyword in the Options line of the Calculations dialog.
If you continue to have difficulty you will have to adjust some of the internal parameters to the multi-step SCF logic. The most common problem areerrors with "level-2" iterations. By default this fails after 75 steps. This can be increased with the D_SCF_MAX_2= keyword. A list of other NMR related keywords can be found in the keyword table below.
In Spartan we report a DP4 score for NMR comparison with experiment. This refers to the DP4. Note that in this context DP4 refers to the statstical measure, not one of the (many) DP4 recipies. In the following there are 3 descriptions for varying levels of detail:
Amore detailed description:
The score used for alignment is designed to be 1 for a perfect fit and 0 for a terrible fit. For a system with N centers:
'ri' is the i'th center of the trial molecule, and 'roi' is the corresponding center of the template molecule. G is a function which behaves like the usual Hookean spring for small values. (~(ri-roi)2) but approaches 1 as the difference in distances (ri-roi) goes to infinity
The second equation is used when (ri-roi)/Ri is greater than 1.0. The normalizing Ri is (3/5) of the van-der-Wall radii for atoms, and for CFD's is the radii given in the property panel when a CFD is selected.
The distinguishing feature of this function when compared to a simple RMSD type function (ri-roi)2 is that in the case where most of the centers will line up exactly, but only 1 is nowhere near matching, the latter center will adversely affect the alignment of the former centers. As an example, let's try to map the H2 molecule onto a template of the Br2 molecule with RBr set anomalously small, say 1/10 of an angstrom. The 'best' (and only) minima found by the RMSD function is the H2 molecule centered symmetrically at the center of the Br2 molecule. The score we use would find an off-center minima with one hydrogen directly on one Bromine, and the other Hydrogen near the center of the Br2 molecule.
When aligning two separate sets of centers, a number of alignments are examined. It should be noted that the 6-dimensional translation/rotation space of the above function can have many local minima, or alignments. These are minimized and examined, and the best one is returned. Also, a second score is used internally: 'the number of 'matched centers'. This score closely matches the reported score, but any alignment in which some center-pairings do not line up with Ri are rejected, prior to comparing actual score values.
The score used in alignment is used in the similarity task. The similarity task is more time consuming than alignment in that similarity will look at multiple ways of matching two molecules using different atom mappings and/or pharmacophores, and can look at multiple conformations stored in "Similarity Libraries". This score can be displayed in the resulting spreadsheet by typing
Cartesian coordinates are typically given in Ångstroms (Å), but are also available in nanometers (nm) and atomic units (au).
Bond distances are typically given in Å, but are also available in nm and au. Bond angles and dihedral angles are given in degrees (°).
Surface areas are typically given in Å2 and volumes in Å3, but are also available in nm2 (nm3) and au2 (au3).
1 Å = 0.1 nm = 1.889762 au
Total energies from Hartree-Fock, density functional and MP2 calculations are typically given in au, but are also available in kcal/mol, kJ/mol and electron volts (eV).
Heats of formation from semi-empirical calculations and thermochemical recipes are typically given in kJ/mol, but are also available in au, kcal/mol and eV.
Strain energies from molecular mechanics calculations are typically given in kJ/mol, but are also available in au, kcal/mol and eV.
Orbital energies from Hartree-Fock, density functional and MP2 calculations are typically given in ev, but are also available in kcal/mol, kJ/mol and au.
Orbital energies from semi-empirical calculations are typically given in eV, but are also available in kcal/mol, kJ/mol and au.
Energy Conversionsa
| au | kcal/mol | kJ/mol | eV | |
| 1 au | - | 6.275x102 | 2.625x103 | 2.721x101 |
| 1 kcal/mol | 1.593x10-3 | - | 4.184 | 4.337x10-2 |
| 1 kJ/mol | 3.809x10-4 | 2.390x10-1 | - | 1.036x10-2 |
| 1 eV | 3.675x10-2 | 2.306x101 | 96.485 | - |
Electron densities and spin densities are given in electrons/au3.
Dipole moments are given in debyes.
Electrostatic potentials are given in kJ/mol.
Atomic charges are given in electrons.
Vibrational frequencies are given in wavenumbers (cm-1).
Energy:
1 au (Hartree)= me*e^4/h-bar^2
= 4.3597482(26) 10^-18 J *
= 4.35974381(34)10^-18 J (1998 CODATA)
= 627.510 kcal/mol
627.5095602 kcal/mol *
627.50947093 kcal/mol (1998 CODATA [new Na])
1 ev = 1.60217733(49) 10^-19 J *
1 ev = 96.485 kJ/mol
4.184 J = 1 Calorie (a constant)
1 kT (T=300K) ~ 2.495 kJ
Entropy:
1 e.u. = 4.184 J/mol*K
= 1 cal/mol*K
Pressure:
1 kbar = 10^8 Pa
= 986.923267 atm
1 atm = 101.325 k Pa (exact) *
Length:
1 A = 10^-10 m
= 1.8897269 au (old value)
= 1.889725988579 au
1 au (Bohr) = h-bar^2/(me*e^2)
= 0.529177249(24) A *
= 0.5291772083(19) A (new CODATA 1998)
Mass:
1 AMU = 1.6605402(10) 10^-27 Kg (Atomic Mass Unit)
= 1.66053873(13) 10^-27 Kg (new CODATA 1998)
Mass C12 = 12.0 AMU
= 12.0 g/mol/Na
1 mn = 1.67492716(13) 10^-27 Kg (Mass of neutron)
1 mp = 1.67262158(13) 10^-27 Kg (Mass of proton)
1.007276470(12) AMU
1 me = 9.1034897(54) 10^-31 Kg (Mass of electron)
9.10938188(72)10^-31 Kg
0.5109906(15) Mev
Wavenumber:
1 cm^-1 = 2.9979 10^-10 s^-1
= 0.29979 THz
2.19474.7 cm-1= 1 Hartree^-1/2 Bohr^-1 AMU^-1/2
Wavelength: (for light = 1/Wavenumber)
= h*c/Energy (for light)
1 nm = 1239.837/ev (ie. homo-lumo gap)
= 1.9166 10^-4/kJ (Na in energy)
Charge:
1 au = 1 e
= 1.602 10^-19 C
= 2.452 10^-18 esu*cm
Dipole moment:
1 debye(D) = 3.336e-30 C*m
= 0.20824 e*A
1 au = 8.479e-30 C*m
= 2.542e-18 esu*cm
= 2.542 D
Polarizability:
1 au = 14.83e-30 m^3
= 14.83 A^3
Moment-of-Inertia:
I cm^-1 = 60.1997601/I[ AMU*bhors^2 ]
I cm^-1 = 16.8576522/I[ AMU*A^2 ]
*In places where multiple values are listed for a given
conversion, the first is the approximation used in Spartan,
the second is the 'exact' value (as of 1973,
1986 or 1998).
Speed of Light : c : 2.99792458 10^10 cm/s * (exact)
Avogadro's Num. : Na : 6.0221367(36) 10^23 *
Na : 6.02214199(47)10^23 (1998 CODATA)
Gas Constant : R : 8.314510(70) J/K/mol *
R : 8.314472(15) J/K/mol (1998 CODATA)
Boltzmann const. : k : 1.380658(12) 10^-23 J/K *
1.3806503(24) 10^-23 J/K (1998 CODATA)
Planck's const. : h : 6.626075(40) 10^-34 J s *
6.62606876(52)10^-34 J s (1998 CODATA)
6.62607015 10^-34 J s (exact definition 2018)
fine-structure : alpha: 1/137.0359895(61)
7.297352533(27) 10^-3 (1998 CODATA)
*In places where multiple values are listed for a given
conversion the first is the approximation used in Spartan,
the second is the 'exact' value
(as of 1973, 1986 or 1998). No. Data sets using the older constants have been generated
for more than 30 years. To make sure newer versions maintain
backward compatibility we continue to use the older values for
these fundamental constants and conversion factors. Even though
each new digit is an important scientific achievement,
the increased precision is well beneath the noise present in
the chemical measurements Spartan deals with.
Back to Top