Quantum Mechanics Energy FAQ

The G3 method (the most used of the Gx series) is a time consuming recipe for calculating accurate "Heats of Formation" (HOF) from first principles. G3 consists of 10 calculations:

1. HF/6-31G* optimization
2. HF/6-31G* frequency and vibrational free energy
3. MP2(full)/6-31G* geometry calculation
4. MP2 and MP4 6-31G* single points
5. MP2 and MP4 6-31+G(d) single points
6. MP2 and MP4 6-31G(2df,p) single points
7. QCISD(T) 6-31G(d) single points
8. MP2(full)/6-311+(2df almost) single point (the G3large basis set)
9. A spin-orbit correction term.
10. An empirical "higher level correction" for valence electrons

All these energies are combined, along with similar calculations done for each atomic species. The result is then subtracted by experimental energies of the "standard state atomically pure" systems to arrive at a good approximation for the actual HOF. A quick overview of how these steps are used can be found in our discussion of calculating the exact energy.

Note that each of these steps is relatively time consuming and practical only for very small systems. The G3(MP2) method is often more than twice as fast, but still prohibitively time consuming for all but small molecules.

The reference to the G3 papers can be found at the end of this FAQ.

The T1 method is a simpler recipe to calculate the absolute heat of formation. It is similar in concept to the G3 method but replaces the post MP2 calculations with empirical relations based on Mulliken bond order and implements a faster MP2 approximation. Thus it is much faster than G3 or G3(MP2) and can be applied to much larger molecules. The steps of the calculation are:

1. HF/6-31G* optimization
2. RI-MP2/6-311+G(2d,p)[6-311G*] single point energy. This is a dual basis set approximation to the MP2 energy
3. An empirical correction using the HF/6-31G* Mulliken bond orders to capture the majority of post MP2 energy, and bond vibrational energy.

The quantum mechanical calculations in Spartan assume that molecules are isolated, with a temperature of zero Kelvin, and with stationary nuclei. Real experiments are carried out with vibrating molecules at finite temperature (often 298.15 K). In order to correct for these differences Spartan can use calculated frequency data to determine a set of normal-mode vibrational frequencies (v_i). (These are the same data used to generate IR spectra.)

Using this approximation, energy corrections are fairly straightforward. Splitting the Enthalpy correction into four (4) parts to include the 'Zero point energy' (Zp), the temperature correction (Hv), enthalpy due to translation (Ht) , and enthalpy due to rotation (Hr).

Note that for small molecules this is a very good approximation. However as molecules get larger the 'normal-mode' approximation becomes less valid. For example:

• floppy side groups, (such as methyl rotors) behave like a 3 well system, not the single well assumed in the normal-mode approximation,
• anharmonic effects become more important,
• large scale flexing motion, which is difficult to accurately calculate, begins to dominate the energy correction.
• conformational flexibility becomes an issue which (energetically) may be more important than the vibrational temperature correction (Hv).

These problems are magnified if one is examining the entropy or free energies of larger molecules. For these reasons low frequency vibrations are often systematically ignored.

The entropy in Spartan is calculated from the same data as vibrational enthalpy (Hv). The equation for entropy (S) can be written as follows:

The constants u_i are proportional to the vibrational frequencies and v_A are inversely proportional to the moment of inertia of the rigid body. It is important to note that these equations ignore any entropy due to conformational flexibility, which may dominate for larger molecules. Also note that low frequency vibrations will dominate the calculation of entropy. It is these modes which break the normal mode assumption, thus making entropy calculations of larger molecules suspect.


Return to Top

You can use the isodesmic proton transfer reaction relative to a standard to calculate the relative basicities. For example if we choose the ammonia molecule as a standard we would write:

where B is the compound of interest. Then the relative proton affinity is:

Relative proton affinity is a measure of the basicity which can easily be converted to pH. In our methods book (table 6-17) we show the accuracy of this calculation for a number of methods and basis sets for series of Nitrogen Bases. A regression analysis shows that even simple HF/6-31G* methods provide results with an accuracy of less than 4 kcal/mol on a system covering 125 kcal/mol range.

There is also an interesting example of predicting pKa's from the graphical map of the electrostatic potential. This can be found on page 478 of A Guide to Molecular Mechanics and Quantum Chemical Calculations.

The pH of a compound should be related the energy (enthalpy) of the reaction described above

If you know the pH of a few standards you can use these in a regression fit (using regression tools in Spartan's spreadsheet). This will result in a simple linear relation correlating 'energy' with 'pH'.

While pK_a's can be calculated using methods described above for pH and basicity it is often possible for to use empirical relationships. For example the Groups of Organic Molecules tutorial (menu  > Tutorials) has an example of determining the pK_a of carboxylic acids from the electrostatic potential of the acidic hydrogen. With a simple linear regression one can get rather good prediction for a rather limited case of molecules. As is shown in the first plot below which is the result of going through the above mentioned tutorial.

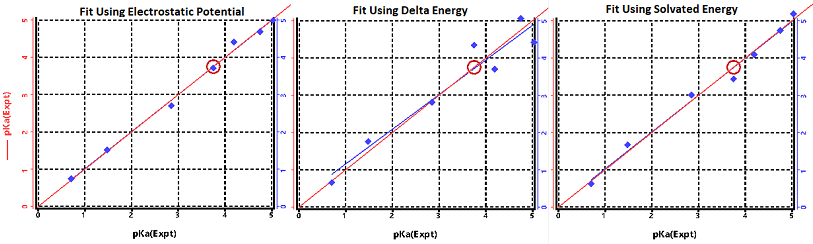
For many cases empirical rules such as this work "good enough" and are so quick to calculate that this is the recommended approach. In principle we calculate the pK_a from first principles using the deceptively simple equation

However, using the fact that the change in energy should be proportional to the energy of de-protonation one can do some quick calculations to approximate pK_a's. The second plot in figure above is a linear fit of the same carboxylic acids but calculate the energy difference between the neutral acid, and the de-protonated acid. In this example the geometry used was the same as the neutral case, except the acid hydrogen was removed. In some cases this kind of fit might be "good enough". The third fit is a similar calculation but done in solvent.

Science is a series of approximations. The trick is to use the largest simplification one can and still get reasonably 'good' predictions. This said, we always feel more comfortable with a theory if a recipe exists to get the *exact* answer. In QM calculations this is so prohibitively time consuming as to be impossible, but it can be described. We describe this 'exact' calculation in the next section.

One definition of the *best* energy is the energy which answers one's questions with enough accuracy, yet consumes the minimum amount of time and resources. As mentioned in the discussion on calculating heats of reactions, this is often achieved by writing a near-isodesmic reaction and calculating an energy difference. (The key here is the 'energy difference'. It allows cancellation of systematic errors.)

In order to find what is *best* for your question, we suggest starting with a question/reaction in which you know the answer and that is similar to your reaction of interest. Try this reaction with HF/6-31G* or HF/3-21G*. If that isn't accurate enough then add the zero-point energy (ZPE) corrections. (scaled by .90 for HF or by .99 for DFT) If that fails, try MP2 or DFT energies with larger basis sets. If that fails attempt single point CCSD with ZPE corrections. Finally try the T1, G3(MP2), or G3 methods.

Conversely, if HF/6-31G* is good enough, you may want to try faster methods to see if they are also acceptable. HF/3-21G* is a popular basis set and much faster than 6-31G*. Semi-Empirical is the simplest method using quantum mechanics approaches while requiring an order of magnitude fewer resources and time. Molecular mechanics methods, while limited to ground states of common chemistry groups, is extremely quick and in the areas in which it is parameterized can be fairly accurate.

If you are new to molecular modeling, Wavefunction's guide book, discusses many types of reactions and molecular properties, quantitatively comparing many different theory levels.


Return to Top

The complete Enthalpy (H) and the Gibb's Free Energy (G) of a given conformer of a molecule in the dilute gas phase can be written

• Ee is the complete electronic energy including
  • an infinite basis set.
  • including all electron correlation (a full CI calculation)
  • accounting for spin-orbit coupling and relativistic effects.
• Zo is the zero point energy of the nuclei.
• Hv is the enthalpy due to vibrations (beyond the zero point energy).
• Sv is the entropy due to vibrations.
• Ht, Hr, St and Sr are the enthalpy and entropy due to rigid body rotation and translation.

Calculating all of these terms is impossible for the foreseeable future for any real/non-trivial molecule. However a number of methods and recipes have been proposed that attempt to approach this limit. Below we describe such an algorithm using the G3 method. The G3 method is a specific thermochemical recipe available in Spartan that attempts to produce accurate results in a relatively short amount of time. By studying it we can generalize it to imagine a method which should give the *exact* results even if such a recipe is impractical.

Below is the edited result of a G3 run on a water molecule, used as a reference:

 Energy  HF/6-31G(d)             -76.009809  1
 Energy MP2/6-31G(d)             -76.196848  2
 Energy MP4/6-31G(d)             -76.207326  3
   perturbation correction        -0.000565  4
   polarization correction        -0.074488  5
   diffuse correction             -0.012979  6
   basis set correction           -0.081653  7
   spin-orbit correction           0.000000  8
   electron pair HLC              -0.025544  9
   ----------------------  ------------------ 
 G3 energy (Ee)                  -76.402556 
   HF/6-31G(d) zero point          0.020515  11
 G3 energy (Eo)                  -76.382040 
   HF/6-31G(d) Vibrational         0.020518  12
   HF/6-31G(d) Translation         0.001416  13
   HF/6-31G(d) Rotational          0.001416 
   RT constant                     0.000944 
 G3 kT energy (H298)             -76.378260 
   Atomic Energy                 -76.032990  14
 dH(298)                          -0.091381 
 dH(298)                         -57.34 kCal/mol

A description of successive improvements to the energy is provided. The details of each step are not discussed here, as the main point is to provide an overview of what is required for an *exact* answer.

1. First we start with the HF energy using the 6-31G(d) basis set. This is the total energy required to pull the 10 electrons, 2 protons, and 1 Oxygen nuclei apart.

2. MP2 can often correct for 80% of this energy. (G3 minimizes the coordinates at the MP2 level. All further energies are done with this geometry.)
3. MP4 is an improvement to MP2 collecting almost 95% of the total correlation energy.
4. In an attempt to do better than 95% of the correlation energy (from MP4), another correction, the "perturbation correction", is made. (G3 theory uses a QCISD calculation for this term).

One weakness in the approach described so far is the basis set. There are a number of possible improvements that can be made to the basis set:

5. Adding polarization terms is often the easiest way to improve a basis set.
6. Diffuse functions are sometimes useful, especially for negatively charged systems.
7. We also need to make the core basis set more flexible with additional terms.
8. We have so far totally neglected any spin-orbit contributions to the energy so we may want to add this energy term in.
9. There are other systematic electronic errors. The G3 method lumps these into a "High Level Correction" (HLC) term.
10. We could also add relativistic effects to the energy although this is not done in the G3 method.

If we carry all the above corrections correctly to their infinite limit we should have the *exact* electronic energy. We label this energy Ee. But this would still not be good enough. We've made the assumption that the nuclei do not move. Quantum mechanics tells us that everything is moving, even at absolute zero; the so called "zero point" energy (Zo). By doing a normal mode analysis we can calculate this zero point energy.

11. G3 calculates this zero point energy at the HF level with the 6-31G(d) basis set. If we had infinite computational resources we could improve this in the same way we discussed improving the electronic energy.

The above energy would be correct at zero Kelvin, but chances are that the system we are studying exists at a non-zero temperature. We can make normal mode corrections to the energy, which we now call enthalpy and label it H298. (298.15 K being the most common temperature of interest.)

12. G3 adds the enthalpy (Hv) due to normal mode vibrations.
13. G3 also adds energy due to translating and rotating the entire molecule, as well as a pressure term from the ideal gas law equation (RT==PV).

At this point we notice that the energy is in some "strange" units called Hartrees. In order to compare with other results it is useful to do a conversion.

14. G3 does an energy conversion to kcals, attempting to define zero using the standard states of the constituent atoms. This finally is dH (delta-H). This is the final goal of the G3 theory.

    This final conversion step is not always necessary. What is necessary in QM calculations is to ensure that when comparing energies, the energies are not only in the same units, but define the same zero. (Typically that means the same basis set and theory level, and molecules with the exact same constituents and number of electrons.)

Often, when examining reactions we require even more; the Gibbs free energy (G) which is calculated by subtracting entropy: G = H - TS + PV.

15. A first approximation of the entropy (S) can be calculated using the same frequency data as Hv was previously.
16. In our calculation of H298 and S we have used the normal mode approximation ignoring anharmonic terms. These actually become important at higher temperature, and are often most noticeable in the calculation of the entropy. Anharmonic cross terms may also become important. For low frequency vibrations the normal mode approximation may not be appropriate and other equations may need to be examined to model rigid rotors (such as methyl groups) or low frequency bending and folding modes.
17. For flexible molecules it is necessary to look at multiple conformers of the same molecule. In a goal to get the *exact* answer one would need to apply all the previously discussed steps to each conformer and weight their contributions using a Boltzmann weighting scheme.

The above steps should cover all the physics of a completely isolated molecule. (i.e. In a vacuum or a dilute gas.) Adding a real environment (such as a solvent or a crystal lattice) is vastly more difficult.

18. Calculating this environment could be attempted by adding a shell of the environment's atoms surrounding the molecule and performing all of the previous steps on this larger system.

Combining all of these corrections terms "correctly" (for which there is currently no 'good' systematic procedure) one should arrive at the "exact" answer.

Thankfully, a careful examination of the types of chemistry questions one typically asks shows that one does not need to do all this work. (See our guide book for a thorough discussion of this.) Surprisingly, in many cases, HF/6-31G(d) is a good approximation to reality. This happy accident makes quantum chemistry possible on today's computers.

Spartan gives users the ability to choose from a number of advanced correlated methods, and implements the G3 recipe, which is a standard approach for improving the accuracy of calculated energies.

Spartan also provides the flexibility to work with a wide variety of theoretical models:.

• Steps 2-4: A number of post HF methods are available, including
  • DFT: BP, EDF2, B3LYP, M06, wB97X-D, wB97X-V (and many more)
  • MP2, RI-MP2, , and MP3
  • CCD, VOD, VQCCD, QCISD, CCSD, OD, QCCD
  • MP4SDQ, MP4
  • QCISD(T), CCSD(T), OD(T)
  • VQCCD(2), VOD(2), QCCD(2), CCSD(2), CCD(2), OD(2)
• Steps 5-7 Spartan has a full range of basis sets available, and allows the input of external basis sets. These include:
  • STO-3G,3-21G(*)
  • 6-31G with flexible polarization and diffuse options.
  • 6-311G with flexible polarization and diffuse options.
  • cc-pVDZ, cc-pVTZ, cc-pVQZ, cc-pV5Z
  • the def2 series of basis sets
  • the G3 basis sets; G3MP2large, G3large
  • ECP basis sets including LACVP and LANL2DZ
  • and the ability to add user basis sets.
• Steps 11-15 The ability to calculate frequencies and other thermodynamic data allows for the calculation of free energy due to vibrations using the normal mode approximation.
• Step 17 Spartan's conformation module makes it easy to generate and work with multiple conformers.
• Step 18 Spartan has a number of solvation methods which can be used to approximate a solvent.

All three approaches have a different definition of zero, and use different units (by convention).

• Molecular Mechanics calculates a "strain" energy. The zero of this system is one in which all bond angles and lengths are at their 'ideal' values. This 'zero' may not be attainable. For example, the water molecule has a 'zero' energy at the global minimum, however, methane does not (in MMFF). This is because in methane the 'unstrained' angle is not 104.9 even though the 3-dimensional interactions of the 6 angles cause the minimized structure to have bond angles of 104.9.

  Given this definition one cannot compare molecular mechanics energies of different molecules. This restriction holds true even for different isomers. One can compare energies of different conformations. In fact this is one of the most popular and appropriate uses of molecular mechanics.

• Semi-Empirical methods use the same definition as ab initio, but a constant is subtracted for each atom in the molecule. The goal of this 'shift' is to approximate a heat of formation (HOF). In reality, this approximation is not very accurate and should only be used as a first guess at the HOF. Semi-Empirical methods are most useful for predicting rough geometries and transition states quickly.

• Ab initio methods (including HF and DFT) compare the energy of the combined molecule with the energy required to remove every electron, and separate every nuclei. While this reaction is not a very realistic experiment, it is theoretically simple and can be used to calculate energy differences of conformers, isomers, and entirely different molecules. See the discussion on calculating the heat of formation for a more detailed description of using this energy.

  By convention ab initio results are returned in units of Hartrees. See the units section to convert from Hartrees to more common units

Each method is different, but an overly short answer would be:

• no parameters for ab initio methods (HF, MP2, MP4, CCSD, ...)
• about a dozen parameters for DFT methods (SVWN, B3LYP, wB97X-D, ...)
• dozens for Semi-Empirical methods (AM1, PM3, ...)
• hundreds for molecular mechanics methods (SYBYL, MMFF, ...)

For an exact number one will need to examine the primary literature on these methods. However, slightly more detailed discussion of these methods presented below. More details can be found in Spartan's documentation.

• The HF, MP2, MP4, CISD, CISD(T) can be thought of as keeping more terms in a "Taylor-like" series expansion of the full/exact quantum mechanical calculation. They are called 'ab initio' because there are no parameters other than where to/how to stop the expansion.
• The basis sets (3-21G*, 6-31G* ...) can be thought of as a "Taylor-like" series expansions of the exact electron density. The smallest have ~10 terms per atom ... and more are added as the sets get bigger. The authors of these basis sets would not call them free parameters, but defend that most of these parameters are derived and claim there are only a few free parameters that describe how the expansion is terminated. (In QM parlance; splitting and polarization.)
• DFT methods can be considered an extension to HF methods, with a few parameters added to attempt to go from HF to the exact quantum mechanical solution. In reality these approximations appear to improve the base HF to MP2 level or better.
• Semi-Empirical, is a radically abbreviated "Taylor-like" expansion of the exact quantum mechanical solution. To compensate for how bad this early termination is, about 20 parameters per atom are added.
• Mechanical force fields are purely empirical; roughly 5 parameters per "atom type", many more for each bond, (including torsional, bond bending, cross terms). In modern force fields there are more "atom types" than one might initially guess. For example, MMFF94 has 8 different kinds of oxygen. Using the PRINTLEV=4 keyword will dump the parameters for a given molecule. (Only available for the molecular mechanics module).

References: